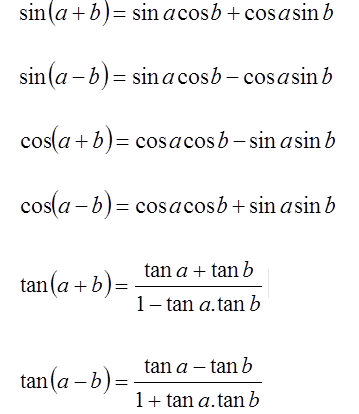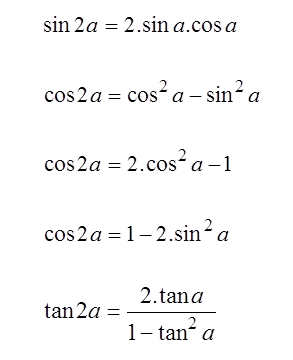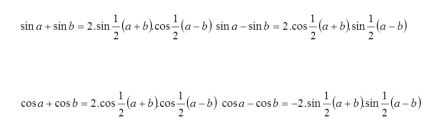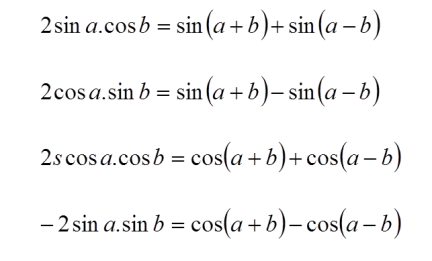Trigonometri
Materi
Jumlah & selisih sudut:
Sudut rangkap:
Jumlah atau selisih à perkalian:
Perkalian jumlah atau selisih:
Contoh soal dan pembahasan
Soal No. 1
Dengan menggunakan rumus penjumlahan dua sudut tentukan nilai dari:
a) sin 75°
b) cos 75°
c) tan 105°
Dengan menggunakan rumus penjumlahan dua sudut tentukan nilai dari:
a) sin 75°
b) cos 75°
c) tan 105°
Pembahasan
a) Rumus jumlah dua sudut untuk sinus
a) Rumus jumlah dua sudut untuk sinus
| sin (A + B) = sin A cos B + cos A sin B |
sin 75° = sin (45° + 30°)
= sin 45° cos 30° + cos 45° sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4 (√6 + √2)
b) Rumus jumlah dua sudut untuk cosinus
= sin 45° cos 30° + cos 45° sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4 (√6 + √2)
b) Rumus jumlah dua sudut untuk cosinus
| cos (a + B) = cos A cos B − sin A sin B |
cos 75° = cos (45° + 30°)
= cos 45° ⋅ cos 30° − sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4 (√6 − √2)
c) Rumus jumlah dua sudut untuk tan
= cos 45° ⋅ cos 30° − sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4 (√6 − √2)
c) Rumus jumlah dua sudut untuk tan
tan 105° = tan (60° + 45°)

Soal No. 2
Dengan menggunakan rumus selisih dua sudut tentukan nilai dari:
a) sin 15°
b) cos 15°
c) tan (3x − 2y)
Pembahasan
a) Rumus selisih dua sudut untuk sinus
Soal No. 2
Dengan menggunakan rumus selisih dua sudut tentukan nilai dari:
a) sin 15°
b) cos 15°
c) tan (3x − 2y)
Pembahasan
a) Rumus selisih dua sudut untuk sinus
| sin (A − B) = sin A cos B − cos A sin B |
sin 15° = sin 45° − 30°)
= sin 45° ⋅ cos 30° − cos 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4(√6 − √2)
b) Rumus selisih dua sudut untuk cosinus
= sin 45° ⋅ cos 30° − cos 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 − 1/2 √2 ⋅ 1/2
= 1/4 √6 − 1/4 √2 = 1/4(√6 − √2)
b) Rumus selisih dua sudut untuk cosinus
| cos (A − B) = cos A cos B + sin A sin B |
cos 15° = cos (45° − 30°)
= cos 45° ⋅ cos 30° + sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4(√6 + √2)
= cos 45° ⋅ cos 30° + sin 45° ⋅ sin 30°
= 1/2 √2 ⋅ 1/2 √3 + 1/2 √2 ⋅ 1/2
= 1/4 √6 + 1/4 √2 = 1/4(√6 + √2)
c) Rumus selisih sudut untuk tan
Sehingga

Soal No. 3
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 4/5 dan sin B = 12/13. Sudut A adalah sudut tumpul sedangkan sudut B adalah sudut lancip. Tentukan:
A. sin (A + B)
B. sin (A − B)
Pembahasan
Gambar segitiga untuk cek nilai sin dan cos kedua sudut, tentunya setelah itu aplikasikan rumus phytagoras untuk mendapatkan panjang sisi-sisi segitiga, seperti gambar berikut:

Nilai sin dan cos "sementara" untuk masing-masing sudut terlihat dari segitiga di atas. Dibilang sementara karena setelah itu kita harus tentukan positif atau negatifnya. Setelah dicocokkan dengan kuadrannya barulah didapat nilai sin atau cos yang benar.
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 4/5 dan sin B = 12/13. Sudut A adalah sudut tumpul sedangkan sudut B adalah sudut lancip. Tentukan:
A. sin (A + B)
B. sin (A − B)
Pembahasan
Gambar segitiga untuk cek nilai sin dan cos kedua sudut, tentunya setelah itu aplikasikan rumus phytagoras untuk mendapatkan panjang sisi-sisi segitiga, seperti gambar berikut:
Nilai sin dan cos "sementara" untuk masing-masing sudut terlihat dari segitiga di atas. Dibilang sementara karena setelah itu kita harus tentukan positif atau negatifnya. Setelah dicocokkan dengan kuadrannya barulah didapat nilai sin atau cos yang benar.
sin A = 4/5
cos A = 3/5
sin B =12/13
cos B = 5/13
cos A = 3/5
sin B =12/13
cos B = 5/13
Periksa ulang,
- Sudut A tumpul sehingga berada di kuadran II (antara 90 dan 180) . Lihat ilustrasi di bawah, untuk kuadran II nilai sin adalah positif, sehingga sin A benar 4/5. Sementara untuk cos A, karena dikuadran II, nilainya negatif, jadi cos A = − 3/5
- Sudut B lancip, sehingga berada di kuadran I (antara 0 dan 90). Baik nilai sin atau cos dikuadran 1 adalah positif, sehingga data di atas bisa langsung digunakan.
a) dari data sin dan cos yang telah diperoleh didapatkan
b) dari data sin dan cos yang telah diperoleh didapatkan
Soal No. 4
Diberikan dua buah sudut A dan B dengan nilai sinus masing-masing adalah sin A = 3/5 dan sin B = 12/13. Sudut A dan sudut B adalah sudut lancip. Tentukan nilai dari cos (A + B)
Pembahasan
Cek nilai sin dan cos dengan segitiga seperti sebelumnya
sin A = 3/5, cos A = 4/5
sin B = 12/13, cos B = 5/13
Kedua sudut adalah lancip hingga baik sin ataupun cos adalah positif semua.
Dari data yang telah diperoleh masukkan rumus untuk cos jumlah sudut
Soal No. 5
Diketahui Δ PQR dengan ∠ P dan ∠ Q lancip. Jika tan P = 3/4 dan tan Q = 1/3, tentukan nilai dari cos R
Pembahasan
Cek sin cos kedua sudut P dan Q
sin P = 3/5, cos P = 4/5
sin Q = 1/√10, cos Q = 3/√10
P + Q + R = 180 atau R = 180 - (P + Q)
cos R = cos (180 - (P + Q))
ingat cos (180 - x) = - cos x

Soal No. 6
Jika tan α = 1, tan β = 1/3 dengan α dan β sudut lancip maka sin (α − β) =....
A. 2/3 √5
B. 1/5 √5
C. 1/2
D. 2/5
E. 1/5
(UN 2007-2008)
Pembahasan
tan α = 1, jika digambarkan dalam sebuah segitiga seperti berikut:

Dari gambar terlihat:
sin α = 1/ √2
cos α = 1/ √2
tan β = 1/3, jika digambarkan dalam sebuah segitiga akan diperoleh nilai sin dan cosnya:

Diperoleh
sin β = 1/√10
cos β = 3/√10
Kembali ke soal, diminta sin (α − β) =....
Dengan rumus selisih dua sudut:

Jadi sin (α − β) = 1/5 √5
Soal No. 7
Jika A + B = π/3 dan cos A cos B = 5/8, maka cos (A − B) =....
A. 1/4
B. 1/2
C. 3/4
D. 1
E. 5/4
un hal 102
Pembahasan
Dari rumus selisih dua sudut untuk cosinus:
cos (A + B) = cos A cos B − sin A sin B
Masukkan data soal
1/2 = 5/8 − sin A sin B
sin A sin B = 5/8 − 1/2 = 1/8
Diminta cos (A − B) =....
cos (A − B) = cos A cos B + sin A sin B
= 5/8 + 1/8 = 6/8 = 3/4
Soal No. 8
ABC adalah sebuah segitiga. Jika sin A = 3/5 dan cotan B = 7, maka ∠C = .....
A. 30°
B. 45°
C. 60°
D. 90°
E. 135°
Pembahasan
Dari data sin A = 3/5 dan cotan B = 7 (atau kalau dari tan nya, tan B = 1/7), diperoleh

sin A = 3/5
cos A = 4/5
sin B = 1/5√2
cos B = 7/5√2
Jumlah sudut dalam suatu segitiga adalah 180, jadi A + B + C = 180° atau bisa juga C = 180 − (A + B)
Kembali ke soal, diminta ∠C, kita cari sin C dulu:
sin C = sin [180 − (A + B)]
sin C = sin (A + B), ingat kembali ada rumus sin (180 − x) = sin x
sin C = sin A cos B + cos A sin B

ingat cos (180 - x) = - cos x
Soal No. 6
Jika tan α = 1, tan β = 1/3 dengan α dan β sudut lancip maka sin (α − β) =....
A. 2/3 √5
B. 1/5 √5
C. 1/2
D. 2/5
E. 1/5
(UN 2007-2008)
Pembahasan
tan α = 1, jika digambarkan dalam sebuah segitiga seperti berikut:
Dari gambar terlihat:
sin α = 1/ √2
cos α = 1/ √2
tan β = 1/3, jika digambarkan dalam sebuah segitiga akan diperoleh nilai sin dan cosnya:
Diperoleh
sin β = 1/√10
cos β = 3/√10
Kembali ke soal, diminta sin (α − β) =....
Dengan rumus selisih dua sudut:
Jadi sin (α − β) = 1/5 √5
Soal No. 7
Jika A + B = π/3 dan cos A cos B = 5/8, maka cos (A − B) =....
A. 1/4
B. 1/2
C. 3/4
D. 1
E. 5/4
un hal 102
Pembahasan
Dari rumus selisih dua sudut untuk cosinus:
cos (A + B) = cos A cos B − sin A sin B
Masukkan data soal
1/2 = 5/8 − sin A sin B
sin A sin B = 5/8 − 1/2 = 1/8
Diminta cos (A − B) =....
cos (A − B) = cos A cos B + sin A sin B
= 5/8 + 1/8 = 6/8 = 3/4
Soal No. 8
ABC adalah sebuah segitiga. Jika sin A = 3/5 dan cotan B = 7, maka ∠C = .....
A. 30°
B. 45°
C. 60°
D. 90°
E. 135°
Pembahasan
Dari data sin A = 3/5 dan cotan B = 7 (atau kalau dari tan nya, tan B = 1/7), diperoleh
sin A = 3/5
cos A = 4/5
sin B = 1/5√2
cos B = 7/5√2
Jumlah sudut dalam suatu segitiga adalah 180, jadi A + B + C = 180° atau bisa juga C = 180 − (A + B)
Kembali ke soal, diminta ∠C, kita cari sin C dulu:
sin C = sin [180 − (A + B)]
sin C = sin (A + B), ingat kembali ada rumus sin (180 − x) = sin x
sin C = sin A cos B + cos A sin B
Sudut yang nilai sin nya 1/2 √2 adalah 45°
sumber : http://matematikastudycenter.com/kelas-11-sma/58-11-sma-trigonometri-jumlah-dan-selisih-dua-sudut
Soal 1.
Sin (a-b) / tan a – tan b
= sin a . cos b – cos a . sin b/ sin a /cos a – sin b/cos b
= sin a . cos b – cos a. Sin b / Sin a . cos b – cos a . sin b/ Cos a . cos b
= sin a . cos b – cos a . sin b x cos a. Cos b / Sin a . cos b – cos a . sin b
= cos a . cos b
Soal 2
Jika 0 < x < П/2 dan 2 tan2 x – 5 tan x + 2 = 0, maka nilai dari 2 sin x . cos x adalah ..
Pembahasan :
2 tan2 x – 5 tan x + 2 = 0
(2 tan x -1) (tan x -2) = 0
2 tan x – 1 = 0 tan x = 2
Tan x = ½
Jadi untuk nilai sin x diambil dari perbandingan tan x = ½
Tan x = ½ = sa/mi
Mencari sisi miring menggunakan rumus phytagoras :
Mi = akar 12 + 22
= akar 5
Sehingga nilai sin x = de/mi
= 1/ akar 5
Cos x = 2/ akar 5
Jadi nilai 2 sin x cos x = 2 x 1/akar 5 x 2/akar 5
= 0,8
Soal 3.
Diketahui α 0 sudut lancip dan sin α = 2/3 . Nilai tg α 0 adalah …
Sin x = 2/3 = de/mi
Tg x = de/sa
Untuk mencari sisi samping sudut dengan menggunakan hukum phytagoras :
Sa = akar 32 – 22
= akar 5
Tg x = 2/akar 5
= 2/akar 5 x akar 5/akar 5
= 2/5 akar 5
Soal 4.
Diketahui sin A0 = 12/13 untuk П/2 < A < П. Nilai dari sin (П/2 – A)0 adalah …
Pembahasan :
Sin (П/2 – A)0 = sin A . cos B – cos A . sin B
= Sin 90 . 5/13 – cos 90 . 12/13
= 5/13
Soal 5.
Pada П/2 < a < П, nilai tg a = 2,4. Nilai sin a =
Tg a = 2,4 = 24/10 = de/sa
Karena range sudut antara 900 dan 1800, maka terletak pada kuadran II sehingga nilai tg bernilai negatif.
Tg a = – 24/10 = de/sa
Sin a = de/mi
Untuk mencari sisi miringnya menggunakan hukum phytagoras..
Mi = akar 242 + 102
= akar 676
= 26
Maka nilai sin a = 24/26
Sin a = 12/13
Soal 6
Berikut ini2 senilai dengan sin 125 adalah ….
Sin 1250 sama dengan sin 550
Sin 125 terletak di kuadran II jadi, sin (180 – 125) = sin 550
Soal 7 .
Diketahui segitiga ABC dengan panjang sisi-sisinya a = 9, b = 7, dan c = 8. Nilai cos C = …
c2 = a2 + b2 – 2ab Cos C
64 = 81 + 49 – 2(9) (7) . cos C
64 = 130 – 126 . cos C
64 – 130 = – 126 . cos C
-66 = -126 cos C
Cos C = 66/126
Cos C = 33/63
Jadi nilai cos C = 33/63
Soal 8.
Untuk 0 ≤ x ≤ 360 himpunan penyelesaian dan persamaan akar 2 sin x – 1 = 0 adalah…
Akar 2 sin x – 1 = 0
Akar 2 sin x = 1
Sin x = 1/akar 2
Sin x = ½ akar 2
X = 450 dan 1350
Soal 8.
Untuk 0 ≤ x ≤ 360 himpunan penyelesaian dan persamaan akar 2 sin x – 1 = 0 adalah…
Akar 2 sin x – 1 = 0
Akar 2 sin x = 1
Sin x = 1/akar 2
Sin x = ½ akar 2
X = 450 dan 1350
Hp = 450 dan 1350
Soal 9.
Untuk -180 < x < 180 himpunan penyelesaian dari 2 cos x + akar 3 = 0 adalah….
2 cos x = – akar 3
Cos x = – akar 3/ 2
= -1/2 akar 3
X = 1500 dan 2400
Jadi Hp = 1500 dan 2400
Soal 10.
Pada П/2 < a < П, nilai tg a = 2,4 . Nilai sin a = …
pembahasan : pada soal ini nilai a terletak pada kuadran kedua yaitu antara 900 sampai 1800, maka nilai tg bernilai negatif :
tg a= – 24/10 = de/sa
sin a = de/mi
mencari sisi miring pada kuadran kedua adalah :
mi = akar 242 + 102
= akar 676
mi = 26
maka sin a = de/mi = 24/26
sin a = 12/13
soal 11.
Tg A = P
Cos 2A = ….?
Pembahasan :
Cos 2A = 1 –2 sin2x
Tg = P = de/sa
Mencari sisi miring :
mi = akar p2 + 1
Sin x = p/ akar p2 + 1
Cos 2A = 1 – 2sin2x
= 1 – 2 (p/ akar p2 + 1)( p/ akar p2 + 1)
= 1 – 2p2/p2 + 1
= p2 + 1 – 2p2/ p2 + 1
= – p2 + 1/p2 + 1
Jadi nilai Cos 2A = 1 – p2/ p2 + 1
soal 12.
Pada segitiga ABC diketahui AC = 6 sudut A = 1200 dari sudut B = 300, maka luas segitiga ABC = ….?
Sin B= de/mi
Sin 30 = 6/mi
½ = 6/mi
Mi = 6/ ½
= 12
Cos B = sa/mi
Cos 30 = sa/ 12
½ akar 3 = sa /12
Sa = ½ akar 3 x 12
sa = 6 akar 3
Luas segitiga adalah : ½ a x t
: ½ x 6 x 6 akar 3
: 18 akar 3
soal 13
Segitiga PQR siku-siku di Q. Jika panjang PR = 15 cm dan sec < p = 5/, nilai cos < R adalah …
Pembahasan : …
Sec < P = 5/3
Cos < P = 3/5
Cos < P = r/q
r = cos < P x q
= 3/5 x 15 cm
= 9 cm
r2 = p2 + q2 – 2pq x cos R
81 = 144 + 225 – 2 (12) (15) x cos R
81 = 369 – 360 . Cos R
288 = 360 Cos R
Cos R = 288/360
Cos R = 4/5
soal 14.
Segitiga ABC diketahui sudut A = 750 sudut A = 600 dan sudut C = 450, maka AB : AC adalah
AB/AC = Sin C/ Sin B
AB/AC = Sin 450/Sin 600
AB/AC = ½ akar 2 / ½ akar 3
AB/AC = akar 2 / akar 3
Soal 15.
Diketahui sin x = 0,6 untuk x terletak diantara 900 dan 1800, maka tg x =…
Sin x = 6/10 = de/mi
Tg x = de/sa
Mencari sisi samping adalah ..
Sa = akar 102 – 62
= akar 64
= 8
karena terletak di kuadran II, maka nilai tg x bernilai negatif
tg x = – 6/8
= – 3/4
Soal 16
Diketahui sin α = a ; α sudut tumpul. Maka tan α =
sin α = a = de/mi
untuk mencari sisi samping adalah …
sa = akar 12 – a2
sa = akar 1 – a2
karena sudut tumpul terletak antara 900 dan 1800, maka nilai tg bernilai negatif
jadi, tg x = – a / akar 1 – a2
soal 17.
diketahui tg x = a
sin 2x = ….?
Pembahasan :
Sin 2x = 2 sinx cosx
tg x = a = de/sa
mencari sisi miringnya…
mi = akar a2 + 12
mi = akar a2 + 1
sin x = de/mi
= a /akar a2 + 1
Cos x = sa/mi = 1/akar a2 + 1
Jadi nilai sin 2x = 2 sinx cosx
= 2 x a/akar a2 + 1 x 1/akar a2 + 1
= 2a/ a2 + 1Soal 1.
Sin (a-b) / tan a – tan b
= sin a . cos b – cos a . sin b/ sin a /cos a – sin b/cos b
= sin a . cos b – cos a. Sin b / Sin a . cos b – cos a . sin b/ Cos a . cos b
= sin a . cos b – cos a . sin b x cos a. Cos b / Sin a . cos b – cos a . sin b
= cos a . cos b
Soal 2
Jika 0 < x < П/2 dan 2 tan2 x – 5 tan x + 2 = 0, maka nilai dari 2 sin x . cos x adalah ..
Pembahasan :
2 tan2 x – 5 tan x + 2 = 0
(2 tan x -1) (tan x -2) = 0
2 tan x – 1 = 0 tan x = 2
Tan x = ½
Jadi untuk nilai sin x diambil dari perbandingan tan x = ½
Tan x = ½ = sa/mi
Mencari sisi miring menggunakan rumus phytagoras :
Mi = akar 12 + 22
= akar 5
Sehingga nilai sin x = de/mi
= 1/ akar 5
Cos x = 2/ akar 5
Jadi nilai 2 sin x cos x = 2 x 1/akar 5 x 2/akar 5
= 0,8
Soal 3.
Diketahui α 0 sudut lancip dan sin α = 2/3 . Nilai tg α 0 adalah …
Sin x = 2/3 = de/mi
Tg x = de/sa
Untuk mencari sisi samping sudut dengan menggunakan hukum phytagoras :
Sa = akar 32 – 22
= akar 5
Tg x = 2/akar 5
= 2/akar 5 x akar 5/akar 5
= 2/5 akar 5
Soal 4.
Diketahui sin A0 = 12/13 untuk П/2 < A < П. Nilai dari sin (П/2 – A)0 adalah …
Pembahasan :
Sin (П/2 – A)0 = sin A . cos B – cos A . sin B
= Sin 90 . 5/13 – cos 90 . 12/13
= 5/13
Soal 5.
Pada П/2 < a < П, nilai tg a = 2,4. Nilai sin a =
Tg a = 2,4 = 24/10 = de/sa
Karena range sudut antara 900 dan 1800, maka terletak pada kuadran II sehingga nilai tg bernilai negatif.
Tg a = – 24/10 = de/sa
Sin a = de/mi
Untuk mencari sisi miringnya menggunakan hukum phytagoras..
Mi = akar 242 + 102
= akar 676
= 26
Maka nilai sin a = 24/26
Sin a = 12/13
Soal 6
Berikut ini2 senilai dengan sin 125 adalah ….
Sin 1250 sama dengan sin 550
Sin 125 terletak di kuadran II jadi, sin (180 – 125) = sin 550
Soal 7 .
Diketahui segitiga ABC dengan panjang sisi-sisinya a = 9, b = 7, dan c = 8. Nilai cos C = …
c2 = a2 + b2 – 2ab Cos C
64 = 81 + 49 – 2(9) (7) . cos C
64 = 130 – 126 . cos C
64 – 130 = – 126 . cos C
-66 = -126 cos C
Cos C = 66/126
Cos C = 33/63
Jadi nilai cos C = 33/63
Soal 8.
Untuk 0 ≤ x ≤ 360 himpunan penyelesaian dan persamaan akar 2 sin x – 1 = 0 adalah…
Akar 2 sin x – 1 = 0
Akar 2 sin x = 1
Sin x = 1/akar 2
Sin x = ½ akar 2
X = 450 dan 1350
Soal 8.
Untuk 0 ≤ x ≤ 360 himpunan penyelesaian dan persamaan akar 2 sin x – 1 = 0 adalah…
Akar 2 sin x – 1 = 0
Akar 2 sin x = 1
Sin x = 1/akar 2
Sin x = ½ akar 2
X = 450 dan 1350
Hp = 450 dan 1350
Soal 9.
Untuk -180 < x < 180 himpunan penyelesaian dari 2 cos x + akar 3 = 0 adalah….
2 cos x = – akar 3
Cos x = – akar 3/ 2
= -1/2 akar 3
X = 1500 dan 2400
Jadi Hp = 1500 dan 2400
Soal 10.
Pada П/2 < a < П, nilai tg a = 2,4 . Nilai sin a = …
pembahasan : pada soal ini nilai a terletak pada kuadran kedua yaitu antara 900 sampai 1800, maka nilai tg bernilai negatif :
tg a= – 24/10 = de/sa
sin a = de/mi
mencari sisi miring pada kuadran kedua adalah :
mi = akar 242 + 102
= akar 676
mi = 26
maka sin a = de/mi = 24/26
sin a = 12/13
soal 11.
Tg A = P
Cos 2A = ….?
Pembahasan :
Cos 2A = 1 –2 sin2x
Tg = P = de/sa
Mencari sisi miring :
mi = akar p2 + 1
Sin x = p/ akar p2 + 1
Cos 2A = 1 – 2sin2x
= 1 – 2 (p/ akar p2 + 1)( p/ akar p2 + 1)
= 1 – 2p2/p2 + 1
= p2 + 1 – 2p2/ p2 + 1
= – p2 + 1/p2 + 1
Jadi nilai Cos 2A = 1 – p2/ p2 + 1
soal 12.
Pada segitiga ABC diketahui AC = 6 sudut A = 1200 dari sudut B = 300, maka luas segitiga ABC = ….?
Sin B= de/mi
Sin 30 = 6/mi
½ = 6/mi
Mi = 6/ ½
= 12
Cos B = sa/mi
Cos 30 = sa/ 12
½ akar 3 = sa /12
Sa = ½ akar 3 x 12
sa = 6 akar 3
Luas segitiga adalah : ½ a x t
: ½ x 6 x 6 akar 3
: 18 akar 3
soal 13
Segitiga PQR siku-siku di Q. Jika panjang PR = 15 cm dan sec < p = 5/, nilai cos < R adalah …
Pembahasan : …
Sec < P = 5/3
Cos < P = 3/5
Cos < P = r/q
r = cos < P x q
= 3/5 x 15 cm
= 9 cm
r2 = p2 + q2 – 2pq x cos R
81 = 144 + 225 – 2 (12) (15) x cos R
81 = 369 – 360 . Cos R
288 = 360 Cos R
Cos R = 288/360
Cos R = 4/5
soal 14.
Segitiga ABC diketahui sudut A = 750 sudut A = 600 dan sudut C = 450, maka AB : AC adalah
AB/AC = Sin C/ Sin B
AB/AC = Sin 450/Sin 600
AB/AC = ½ akar 2 / ½ akar 3
AB/AC = akar 2 / akar 3
Soal 15.
Diketahui sin x = 0,6 untuk x terletak diantara 900 dan 1800, maka tg x =…
Sin x = 6/10 = de/mi
Tg x = de/sa
Mencari sisi samping adalah ..
Sa = akar 102 – 62
= akar 64
= 8
karena terletak di kuadran II, maka nilai tg x bernilai negatif
tg x = – 6/8
= – 3/4
Soal 16
Diketahui sin α = a ; α sudut tumpul. Maka tan α =
sin α = a = de/mi
untuk mencari sisi samping adalah …
sa = akar 12 – a2
sa = akar 1 – a2
karena sudut tumpul terletak antara 900 dan 1800, maka nilai tg bernilai negatif
jadi, tg x = – a / akar 1 – a2
soal 17.
diketahui tg x = a
sin 2x = ….?
Pembahasan :
Sin 2x = 2 sinx cosx
tg x = a = de/sa
mencari sisi miringnya…
mi = akar a2 + 12
mi = akar a2 + 1
sin x = de/mi
= a /akar a2 + 1
Cos x = sa/mi = 1/akar a2 + 1
Jadi nilai sin 2x = 2 sinx cosx
= 2 x a/akar a2 + 1 x 1/akar a2 + 1
= 2a/ a2 + 1